定义
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
从带权路径长度讲起
树的带权路径长度(Weighted Path Length of Tree):定义为树中所有叶结点的带权路径长度之和。
结点的带权路径长度:结点到树根之间的路径长度与该结点上权的乘积。
如何计算带权路径长度
对于如下两棵树:
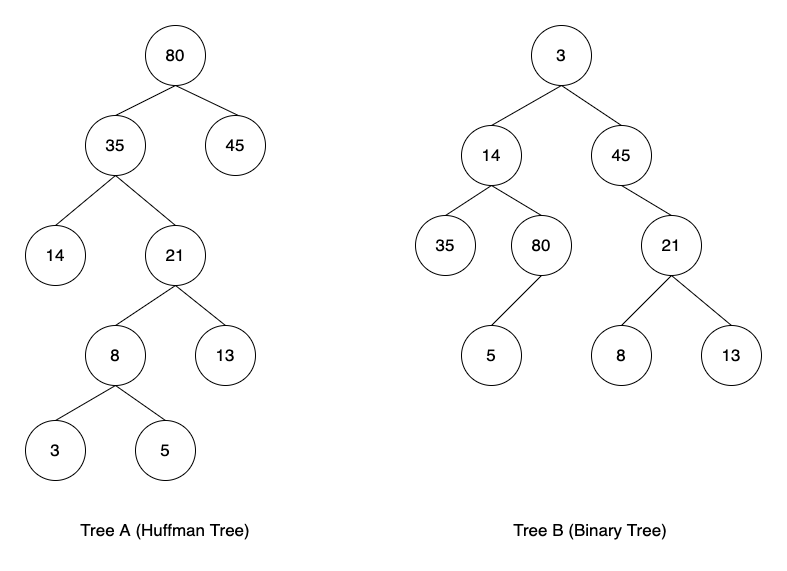
他们的带权路径长度计算方式为:
Tree A : $45\times1+14\times2+13\times3+3\times4+5\times4=144$
Tree B : $35\times2+5\times3+8\times3+13\times3=148$
对于同样的叶子结点,哈夫曼树的带权路径长度最小(以上例子不能证明,请自行证明)
生成一颗哈夫曼树
前面提到,哈夫曼树的带权路径长度最小,也就是说,越靠近根节点,权值越大,另外,左节点的权值小于右节点
我们根据下面这个例子,生成一颗哈夫曼树:
各个字母的权值如下:
| 字母 | 权值 |
|---|---|
| A | 3 |
| B | 45 |
| C | 5 |
| D | 14 |
| E | 13 |
首先,我们可以根据各个权重排序,得到如下节点:
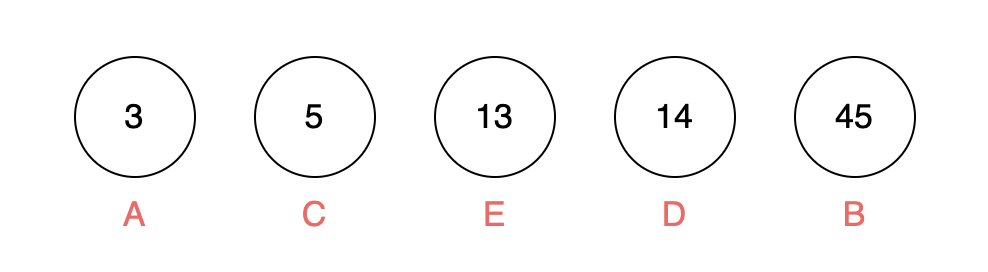
取最小的两个节点作为叶子结点,组成一颗二叉树,其根节点权重为两个叶子结点的权重之和,放回列表中,重新排序:

重复以上步骤,即取权值最小的两个节点作为子结点组成二叉树,其根节点权重为两个子结点的权重之和,放回列表中,重新排序:
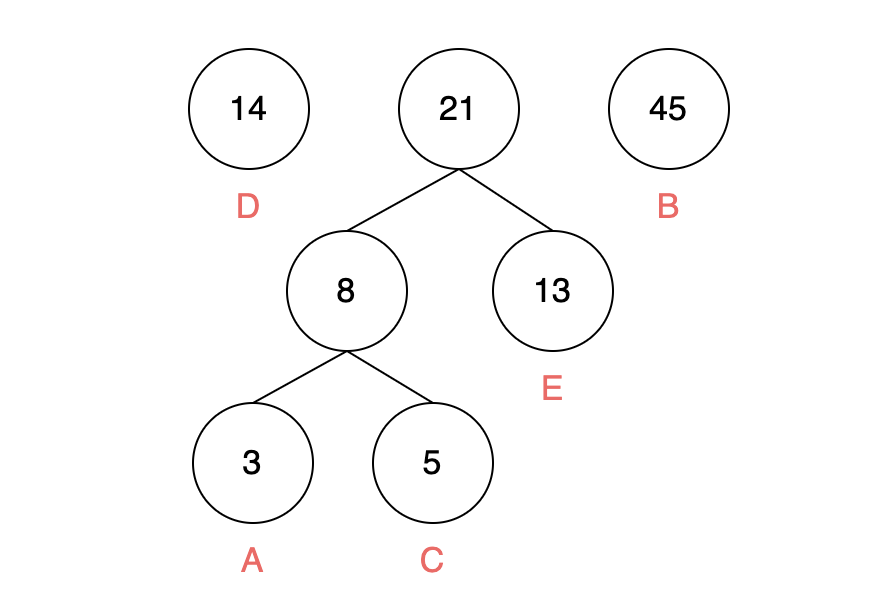
继续重复以上步骤,直到只剩下一个根节点,即生成完成:
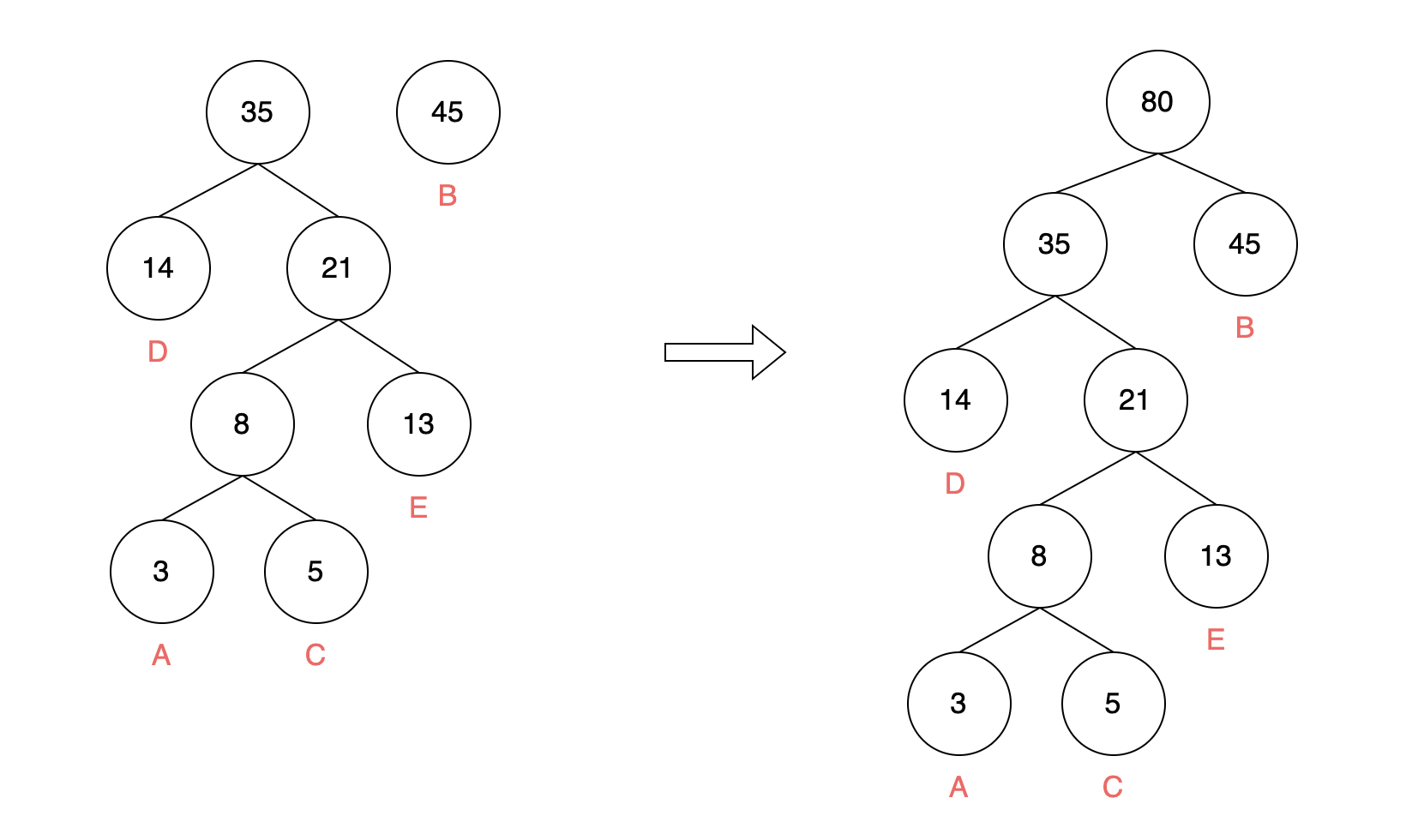
哈夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
如何通过哈夫曼树,找到对应的哈夫曼编码?
非常简单,从根节点出发,左节点为 0,右节点为 1,直至找到叶子结点,遍历的过程即为该节点的哈夫曼编码
对于以上的例子:
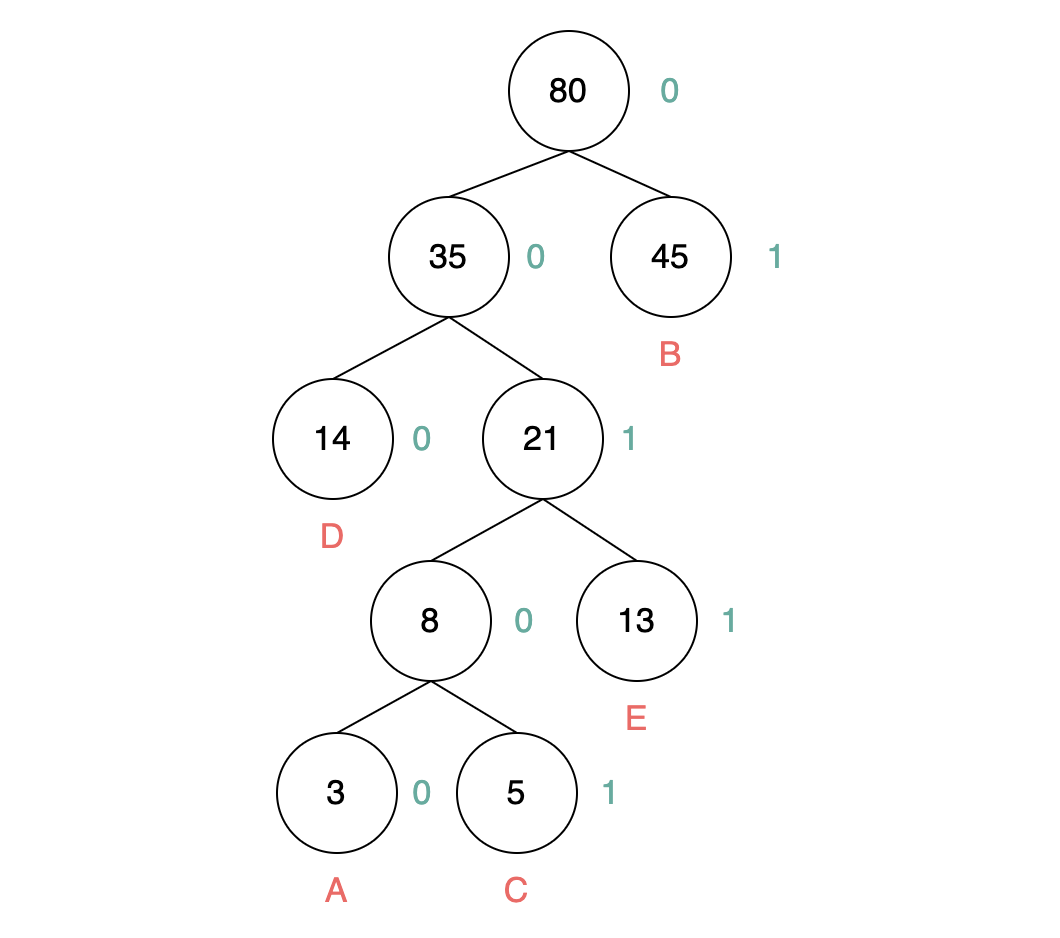
其哈夫曼编码为:
| 字母 | 哈夫曼编码 |
|---|---|
| A | 0100 |
| B | 1 |
| C | 0101 |
| D | 00 |
| E | 011 |
Java实现
节点定义:
public class Node implements Comparable<Node> {
private Byte data; //存放数据本身
private int weight; //权值
private Node left; //指向左子节点
private Node right; //指向右子节点
}构建哈夫曼树:
// 从byte数组构建哈夫曼树
public HuffmanTree(Byte[] bytes) {
// 统计频率
Map<Byte, Integer> frequency = new HashMap<>();
for (Byte b : bytes) {
frequency.put(b, frequency.getOrDefault(b, 0) + 1);
}
// 构造节点list并排序
List<Node> nodeList = new ArrayList<>();
for (Map.Entry<Byte, Integer> entry : frequency.entrySet()) {
nodeList.add(new Node(entry.getKey(), entry.getValue()));
}
Collections.sort(nodeList);
// 构造树
while (nodeList.size() > 1) {
// 取最小的两个,作为左右子节点
Node left = nodeList.get(0);
Node right = nodeList.get(1);
// 创建父节点
Node node = new Node(left.getWeight() + right.getWeight(), left, right);
// 移除子节点
nodeList.remove(left);
nodeList.remove(right);
// 加入父节点
nodeList.add(node);
// 重新排序
Collections.sort(nodeList);
}
// 记录根节点
this.root = nodeList.get(0);
}获取哈夫曼编码:
// 获取哈夫曼编码
public Map<Byte, String> getHuffmanCode() {
Map<Byte, String> huffmanCodes = new HashMap<>();
if (root == null) {
return null;
}
//处理只有root节点的特殊情况
if (root.getLeft() == null && root.getRight() == null) {
huffmanCodes.put(root.getData(), "0");
}
// 用于拼接01字符串
StringBuilder builder = new StringBuilder();
// 处理左子树
getCodes(root.getLeft(), "0", builder, huffmanCodes);
// 处理右子树
getCodes(root.getRight(), "1", builder, huffmanCodes);
return huffmanCodes;
}完整代码
HuffmanTree.java
package org.kakkk.hfmzip.huffman;
import java.util.*;
public class HuffmanTree {
private Node root;
public Node getRoot() {
return root;
}
public void setRoot(Node root) {
this.root = root;
}
// 从byte数组构建哈夫曼树
public HuffmanTree(Byte[] bytes) {
// 统计频率
Map<Byte, Integer> frequency = new HashMap<>();
for (Byte b : bytes) {
frequency.put(b, frequency.getOrDefault(b, 0) + 1);
}
// 构造节点list并排序
List<Node> nodeList = new ArrayList<>();
for (Map.Entry<Byte, Integer> entry : frequency.entrySet()) {
nodeList.add(new Node(entry.getKey(), entry.getValue()));
}
Collections.sort(nodeList);
// 构造树
while (nodeList.size() > 1) {
// 取最小的两个,作为左右子节点
Node left = nodeList.get(0);
Node right = nodeList.get(1);
// 创建父节点
Node node = new Node(left.getWeight() + right.getWeight(), left, right);
// 移除子节点
nodeList.remove(left);
nodeList.remove(right);
// 加入父节点
nodeList.add(node);
// 重新排序
Collections.sort(nodeList);
}
// 记录根节点
this.root = nodeList.get(0);
}
// 获取哈夫曼编码
public Map<Byte, String> getHuffmanCode() {
Map<Byte, String> huffmanCodes = new HashMap<>();
if (root == null) {
return null;
}
//处理只有root节点的特殊情况
if (root.getLeft() == null && root.getRight() == null) {
huffmanCodes.put(root.getData(), "0");
}
// 用于拼接01字符串
StringBuilder builder = new StringBuilder();
// 处理左子树
getCodes(root.getLeft(), "0", builder, huffmanCodes);
// 处理右子树
getCodes(root.getRight(), "1", builder, huffmanCodes);
return huffmanCodes;
}
public void print() {
TreePrinter.printNode(this.root);
}
private void getCodes(Node node, String code, StringBuilder builder, Map<Byte, String> huffmanCodes) {
// 引用传递,需要再new一个防止共用
StringBuilder sb = new StringBuilder(builder);
// 将code加入到StringBuilder
sb.append(code);
// 节点为空,直接返回
if (node==null){
return;
}
// 若data为空,则为非叶子结点,否则为叶子结点
if (node.getData() == null) {
// 递归处理
// 左边递归
getCodes(node.getLeft(), "0", sb, huffmanCodes);
// 右边递归
getCodes(node.getRight(), "1", sb, huffmanCodes);
} else {
// 叶子结点即找到编码,保存
huffmanCodes.put(node.getData(), sb.toString());
}
}
}
Node.Java
package org.kakkk.hfmzip.huffman;
public class Node implements Comparable<Node> {
private Byte data; //存放数据本身
private int weight; //权值
private Node left; //指向左子节点
private Node right; //指向右子节点
public Byte getData() {
return data;
}
public void setData(Byte data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
public Node(int weight, Node left, Node right) {
this.weight = weight;
this.left = left;
this.right = right;
}
// 实现Comparable接口,由小到大排序
@Override
public int compareTo(Node o) {
if (o.getWeight() > this.getWeight()) {
return -1;
}
if (o.getWeight() < this.getWeight()) {
return 1;
}
return 0;
}
@Override
public String toString() {
return "Node [data=" + data + ", weight=" + weight + "]";
}
}TreePrinter.java,用于打印节点(参考:How to print binary tree diagram in Java):
package org.kakkk.hfmzip.huffman;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
class TreePrinter {
public static <T extends Comparable<?>> void printNode(Node root) {
int maxLevel = TreePrinter.maxLevel(root);
printNodeInternal(Collections.singletonList(root), 1, maxLevel);
}
private static <T extends Comparable<?>> void printNodeInternal(List<Node> nodes, int level, int maxLevel) {
if (nodes.isEmpty() || TreePrinter.isAllElementsNull(nodes))
return;
int floor = maxLevel - level;
int endgeLines = (int) Math.pow(2, (Math.max(floor - 1, 0)));
int firstSpaces = (int) Math.pow(2, (floor)) - 1;
int betweenSpaces = (int) Math.pow(2, (floor + 1)) - 1;
TreePrinter.printWhitespaces(firstSpaces);
List<Node> newNodes = new ArrayList<Node>();
for (Node node : nodes) {
if (node != null) {
System.out.print(node.getWeight());
newNodes.add(node.getLeft());
newNodes.add(node.getRight());
} else {
newNodes.add(null);
newNodes.add(null);
System.out.print(" ");
}
TreePrinter.printWhitespaces(betweenSpaces);
}
System.out.println("");
for (int i = 1; i <= endgeLines; i++) {
for (int j = 0; j < nodes.size(); j++) {
TreePrinter.printWhitespaces(firstSpaces - i);
if (nodes.get(j) == null) {
TreePrinter.printWhitespaces(endgeLines + endgeLines + i + 1);
continue;
}
if (nodes.get(j).getLeft() != null)
System.out.print("/");
else
TreePrinter.printWhitespaces(1);
TreePrinter.printWhitespaces(i + i - 1);
if (nodes.get(j).getRight() != null)
System.out.print("\\");
else
TreePrinter.printWhitespaces(1);
TreePrinter.printWhitespaces(endgeLines + endgeLines - i);
}
System.out.println("");
}
printNodeInternal(newNodes, level + 1, maxLevel);
}
private static void printWhitespaces(int count) {
for (int i = 0; i < count; i++)
System.out.print(" ");
}
private static <T extends Comparable<?>> int maxLevel(Node node) {
if (node == null)
return 0;
return Math.max(TreePrinter.maxLevel(node.getLeft()), TreePrinter.maxLevel(node.getRight())) + 1;
}
private static <T> boolean isAllElementsNull(List<T> list) {
for (Object object : list) {
if (object != null)
return false;
}
return true;
}
}测试
测试代码:
package org.kakkk.hfmzip;
import org.kakkk.hfmzip.huffman.HuffmanTree;
public class Main {
public static void main(String[] args) {
Byte[] bytes = {1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,2,2,2,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,5,5,5};
HuffmanTree t = new HuffmanTree(bytes);
t.print();
System.out.println(t.getHuffmanCode());
}
}输出:
80
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
35 45
/ \
/ \
/ \
/ \
14 21
/ \
/ \
8 13
/ \
3 5
{1=1, 2=0100, 3=0101, 4=00, 5=011} 