最近学校数据结构课程布置了一个作业，我觉得很有意思，这里记录一下

题目

布线问题：印刷电路板将布线区域划分为n×m个方格阵列。布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案

要求：

• 布线时电路只能沿直线或直角布线。
• 已布线方格做上封闭标记，其他线路布线不允许穿过封闭区域。（如下图所示）

算法实现

这里使用队列式分支限界法来解决

1. 首先，记录起点步数为0，起点的上下左右中，可达的节点步数为1，并将该坐标其放入队列中，如下图所示：

   

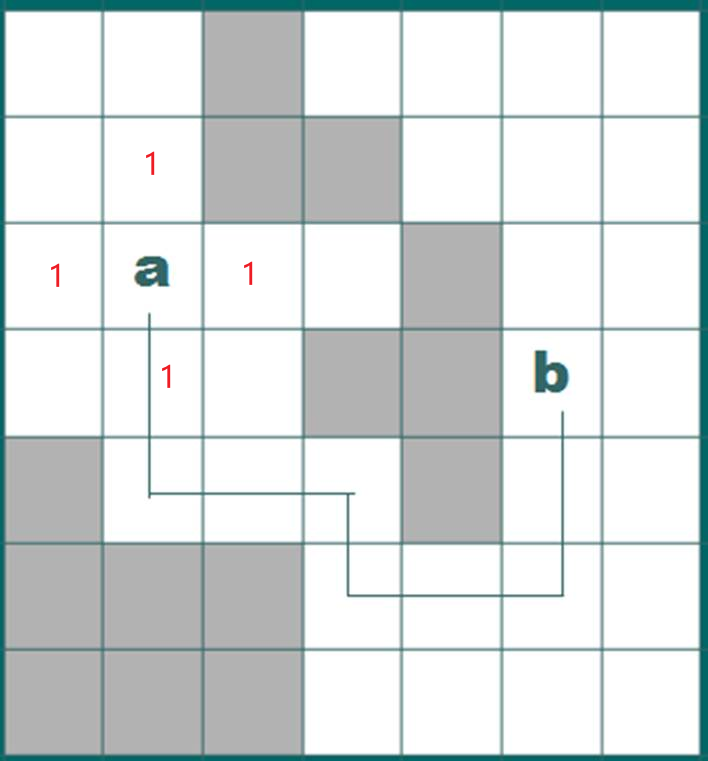
2. 从队列中取出坐标，对与当前坐标，上下左右可达且未被记录的坐标记录步数+1，如下图：

   

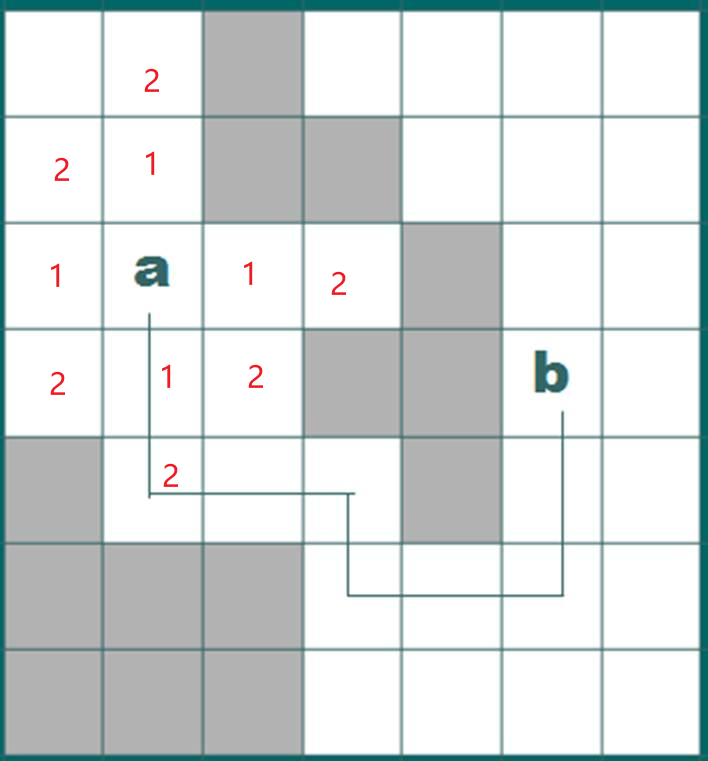
3. 以此类推，直到找到目标坐标：

   

4. 从目标坐标回溯到起始坐标，记录路线即为所求

代码实现（Java）

Position.java

package t2;

public class Position {
    private int row;
    private int col;

    public int getRow() {
        return row;
    }

    public void setRow(int row) {
        this.row = row;
    }

    public int getCol() {
        return col;
    }

    public void setCol(int col) {
        this.col = col;
    }

    public Position(int row, int col) {
        this.row = row;
        this.col = col;
    }

    @Override
    public String toString() {
        return "(" + row + "," + col + ')';
    }
}

Path.java

package t2;

import java.util.LinkedList;

public class Path {
    public static Position[] find(int[][] grid, Position start, Position end) {
        int[][] markGrid = new int[grid.length + 2][grid[0].length + 2];
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                // 此时，markGrid[i][j]: -1 表示不能布线，-2表示未标记
                markGrid[i + 1][j + 1] = grid[i][j] - 2;
            }
        }
        // 添加边界，方便后面不会数组索引越界
        for (int i = 0; i < markGrid.length; i++) {
            if (i == 0 || i == markGrid.length - 1) {
                for (int j = 0; j < markGrid[0].length; j++) {
                    markGrid[i][j] = -1;
                }
            }
            markGrid[i][0] = -1;
            markGrid[i][markGrid[0].length - 1] = -1;
        }

        LinkedList<Position> queue = new LinkedList<>();                                // 任务队列
        markGrid[start.getRow() + 1][start.getCol() + 1] = 0;                           // 起始位置：步数为0
        queue.offer(new Position(start.getRow() + 1, start.getCol() + 1));      // 起始位置入队
        int step = 0;//标记步数
        boolean ok = false;//标记是否成功
        while (true) {
            // 队列为空，说明不可达
            if (queue.isEmpty()) {
                break;
            }

            // 取出任务
            Position curr = queue.poll();

            // 未标记则放入队列，并处理
            // 上
            if (markGrid[curr.getRow() - 1][curr.getCol()] == -2) {
                markGrid[curr.getRow() - 1][curr.getCol()] = markGrid[curr.getRow()][curr.getCol()]+1;
                if (curr.getRow() - 1 == end.getRow() + 1 && curr.getCol() == end.getCol() + 1) {
                    step=markGrid[curr.getRow()][curr.getCol()]+1;
                    ok = true;
                    break;
                }
                queue.offer(new Position(curr.getRow() - 1, curr.getCol()));
            }
            // 下
            if (markGrid[curr.getRow() + 1][curr.getCol()] == -2) {
                markGrid[curr.getRow() + 1][curr.getCol()] = markGrid[curr.getRow()][curr.getCol()]+1;
                if (curr.getRow() + 1 == end.getRow() + 1 && curr.getCol() == end.getCol() + 1) {
                    step=markGrid[curr.getRow()][curr.getCol()]+1;
                    ok = true;
                    break;
                }
                queue.offer(new Position(curr.getRow() + 1, curr.getCol()));
            }
            // 左
            if (markGrid[curr.getRow()][curr.getCol() - 1] == -2) {
                markGrid[curr.getRow()][curr.getCol() - 1] = markGrid[curr.getRow()][curr.getCol()]+1;
                if (curr.getRow() == end.getRow() + 1 && curr.getCol() - 1 == end.getCol() + 1) {
                    step=markGrid[curr.getRow()][curr.getCol()]+1;
                    ok = true;
                    break;
                }
                queue.offer(new Position(curr.getRow(), curr.getCol() - 1));
            }
            // 右
            if (markGrid[curr.getRow()][curr.getCol() + 1] == -2) {
                markGrid[curr.getRow()][curr.getCol() + 1] = markGrid[curr.getRow()][curr.getCol()]+1;
                if (curr.getRow() - 1 == end.getRow() + 1 && curr.getCol() + 1 == end.getCol() + 1) {
                    step=markGrid[curr.getRow()][curr.getCol()]+1;
                    ok = true;
                    break;
                }
                queue.offer(new Position(curr.getRow(), curr.getCol() + 1));
            }
        }
        if (!ok) {
            return null;
        }
        Position[] res = new Position[step];
        Position curr = new Position(end.getRow()+1, end.getCol()+1);
        LinkedList<Position> resQueue = new LinkedList<>();
        resQueue.offer(curr);
        while (markGrid[curr.getRow()][curr.getCol()]!=0){
            // 查找前驱结点
            //上
            if (markGrid[curr.getRow() - 1][curr.getCol()] == markGrid[curr.getRow()][curr.getCol()] - 1) {
                resQueue.offer(new Position(curr.getRow() - 1, curr.getCol()));
                curr = new Position(curr.getRow() - 1, curr.getCol());
                continue;
            }
            // 下
            if (markGrid[curr.getRow() + 1][curr.getCol()] == markGrid[curr.getRow()][curr.getCol()] - 1) {
                resQueue.offer(new Position(curr.getRow() +1, curr.getCol()));
                curr = new Position(curr.getRow() + 1, curr.getCol());
                continue;
            }
            // 左
            if (markGrid[curr.getRow()][curr.getCol() - 1] == markGrid[curr.getRow()][curr.getCol()] - 1) {
                resQueue.offer(new Position(curr.getRow(), curr.getCol()-1));
                curr = new Position(curr.getRow(), curr.getCol() - 1);
                continue;
            }
            // 右
            if (markGrid[curr.getRow()][curr.getCol() + 1] == markGrid[curr.getRow()][curr.getCol()] - 1) {
                resQueue.offer(new Position(curr.getRow(), curr.getCol()+1));
                curr = new Position(curr.getRow(), curr.getCol() + 1);
            }
        }
        for (int i = res.length - 1; i >= 0; i--) {
            Position temp =resQueue.poll();
            assert temp != null;
            // 坐标转化
            res[i]=new Position(temp.getRow()-1,temp.getCol()-1);
        }
        return res;
    }
}

Test.java

package t2;

public class Test {
    public static void main(String[] args) {
        int[][] grid = {
                {0, 0, 1, 0, 0, 0, 0},
                {0, 0, 1, 1, 0, 0, 0},
                {0, 0, 0, 0, 1, 0, 0},
                {0, 0, 0, 1, 1, 0, 0},
                {1, 0, 0, 0, 1, 0, 0},
                {1, 1, 1, 0, 0, 0, 0},
                {1, 1, 1, 0, 0, 0, 0}
        };

        Position[] res=Path.find(grid,new Position(2,1),new Position(3,5));
        if (res==null){
            System.out.println("不可达");
            return;
        }
        for (int i = 0; i < res.length; i++) {
            System.out.println(res[i]);
        }
    }
}