介绍
AVL树(Adelson-Velsky and Landis Tree)是计算机科学中最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logn)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。AVL树得名于它的发明者G. M. Adelson-Velsky和Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
(以上摘自wikipedia)
说白了,就是AVL树具有以下性质:
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
如图就是一颗按照1~10顺序插入的AVL树
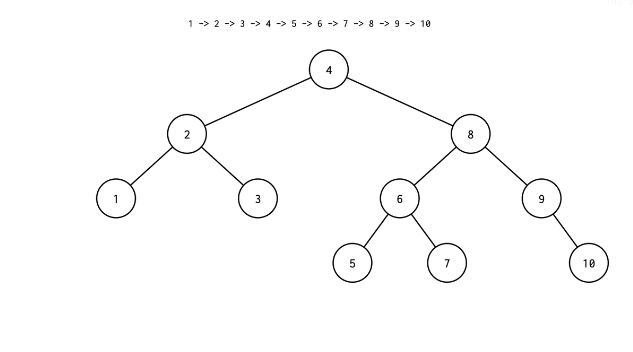
为什么需要AVL树?
通过观察上面那棵树的插入,我们不难发现,如果使用简单的二叉搜索树,插入如果是有序的话,这棵树将退化成一个链表结构,这是我们不想看到的,此时,就需要AVL树这种自平衡的二叉树
相关操作
基础设计
在讲设计之前,我们首先需要引入平衡因子的概念。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
这里我们储存树的高度。
type TreeNode struct {
Value int
Height int //节点高度
Left *TreeNode
Right *TreeNode
}
//获取节点高度
func (node *TreeNode) getHigh() int {
if node==nil{
return 0
}
return node.Height
}插入
在讲插入之前,我们需要了解树的旋转,用于调整树的平衡
左旋
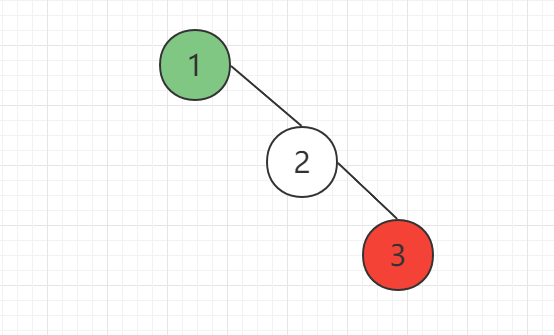
如图所示,当节点插入顺序为1->2->3时,在插入3节点的时候,该树不平衡,此时需要调整树的结构,将2和2节点做父子交换,即2节点为父节点,1节点为2的左子节点,如下图所示:
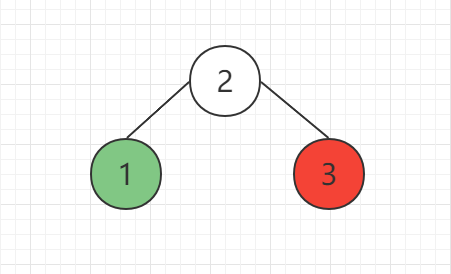
以上属于比较简单的情况,当根节点的右子节点存在左子树时,情况将变得稍微复杂一些,如图所示,在插入6节点后,该树出现不平衡,4节点需要进行左旋操作。
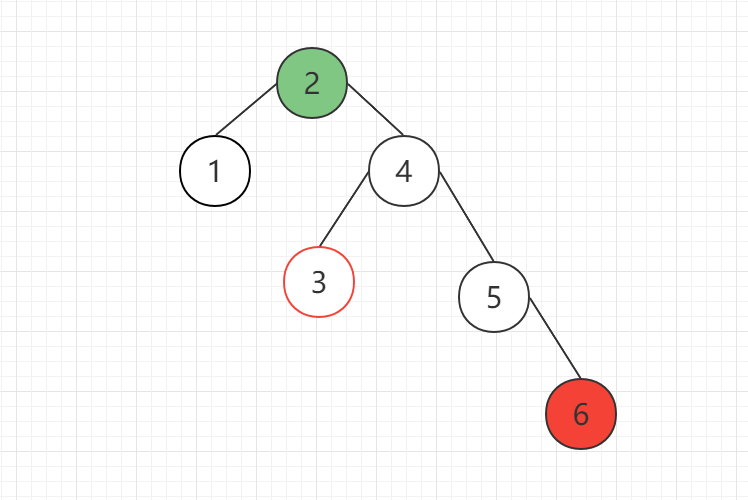
具体操作如下:
- 断开根节点(2)与右子节点(4)的链接,右子节点(4)断开其左子节点(3)的链接
- 4节点提升为父节点,4节点的左子节点为之前的父节点,之前的父节点的右子节点为4节点的前左子节点
(好绕啊,我也说不清楚,看图更实在)
调整后如图所示
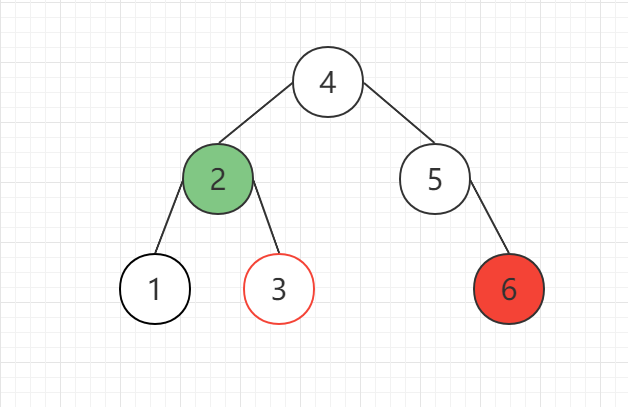
而实际上,情况1与情况2属于同一种情况,可以归为一类,叫做左旋操作
实现代码:
//左旋
func (node *TreeNode) leftRotate() *TreeNode {
root := node.Right //记录新的根节点
node.Right = root.Left //该节点的右子节点为前右子节点的左子节点
root.Left = node //新根节点的左子节点为该节点
//更新节点高度
node.Height = max(node.Left.getHigh(), node.Right.getHigh()) + 1
root.Height = max(root.Left.getHigh(), root.Right.getHigh()) + 1
return root
}右旋
对于右旋操作,其实可以理解为左旋的镜像操作,不做过多赘述,看图就完事了
如图所示,需要进行左旋操作:
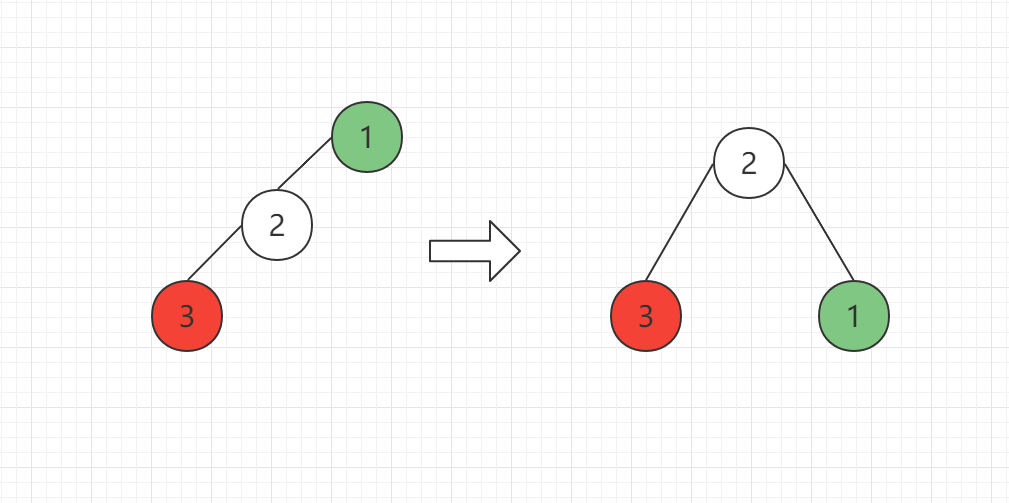
同样的,对于存在子树的情况,如下:
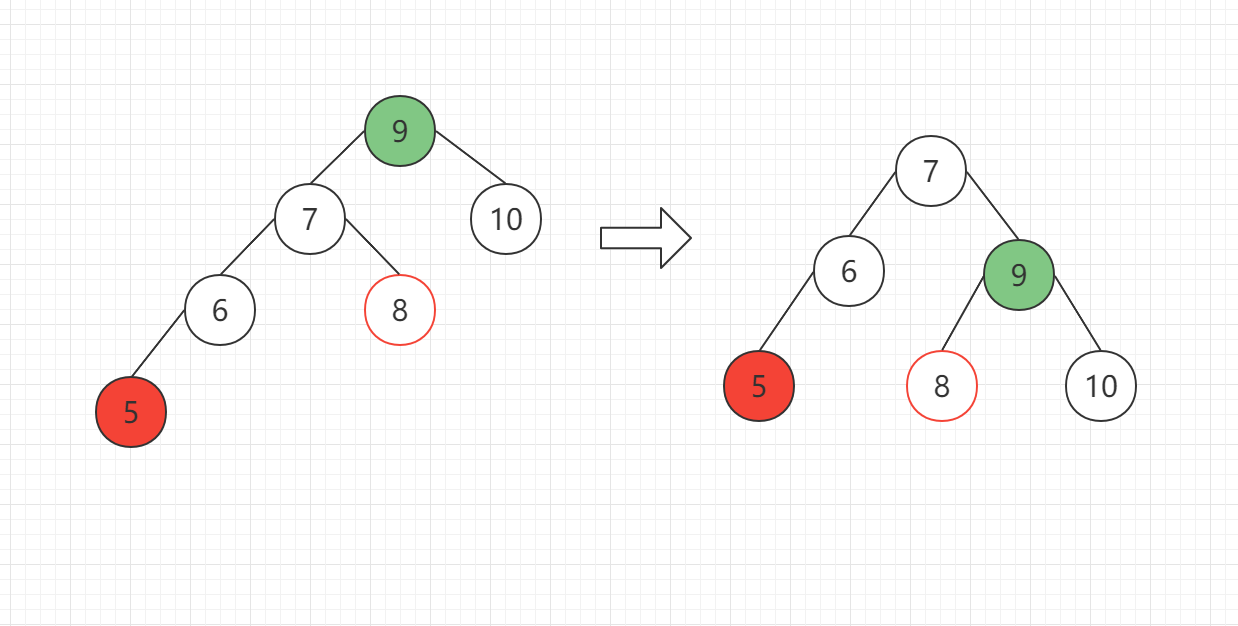
实现代码:
//右旋
func (node *TreeNode) rightRotate() *TreeNode {
root := node.Left //记录新的根节点
node.Left = root.Right //该节点的左子节点为前左子节点的右子节点
root.Right = node //新根节点的右子节点为该节点
//更新节点高度
node.Height = max(node.Left.getHigh(), node.Right.getHigh()) + 1
root.Height = max(root.Left.getHigh(), root.Right.getHigh()) + 1
return root
}先左旋再右旋
如图所示,在下面的树中插入节点9时,会发现,无论是左旋还是右旋,都无法使这棵树再次满足AVL的条件,此时需要做两次旋转操作
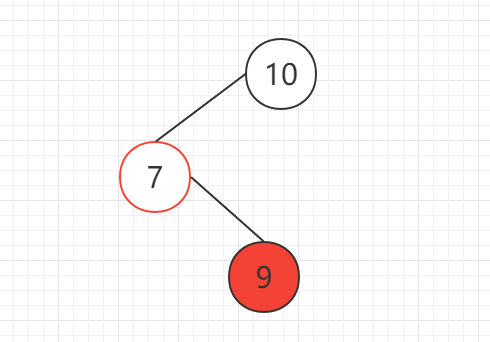
首先,先对节点10的左子节点7做左旋操作,使之变为如下所示:
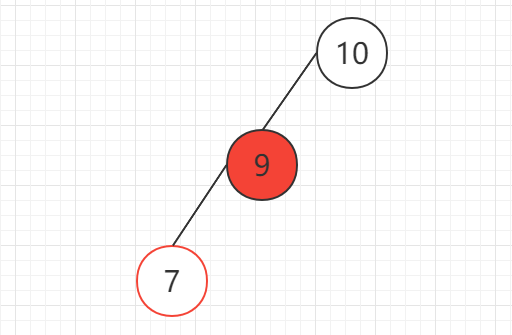
此时,这棵树就变得熟悉了起来,是的没错,对10节点进行右旋操作即可
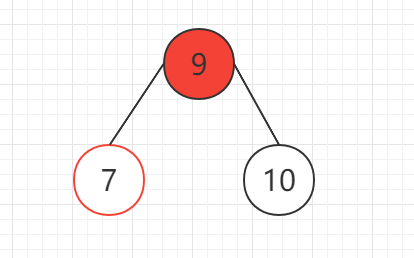
来个复杂的树看看:
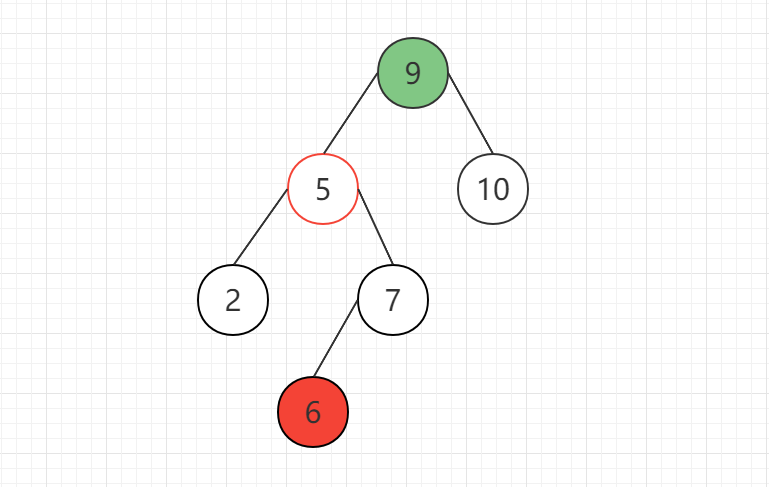
此时对于节点9,不满足AVL树的性质,并且符合先左旋后右旋的条件,因此,先对其左子树进行左旋操作:
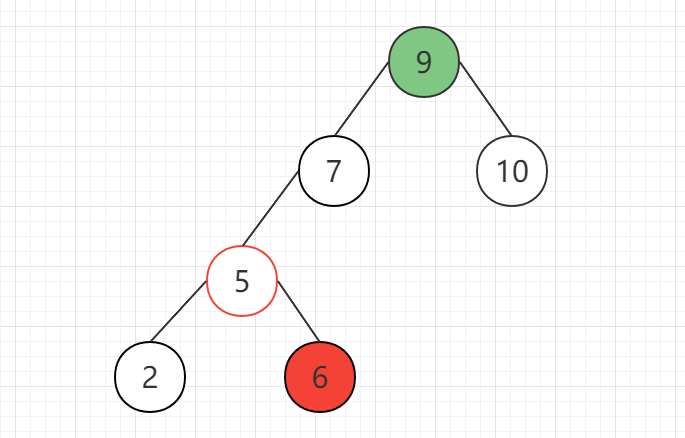
再对节点9本身进行右旋操作:

即可得到满足AVL树条件的一颗树
实现代码
//先左旋再右旋
func (node *TreeNode) leftThenRightRotate() *TreeNode {
afterLRotateNode := node.Left.leftRotate() //记录左节点左旋后的根节点
node.Left = afterLRotateNode //将本节点的左节点设置为左旋后的根节点(完成左旋操作)
return node.rightRotate() //将节点本身右旋并返回
}先右旋再左旋
同样的,这是先左旋再右旋的镜像操作,废话不多说直接上图
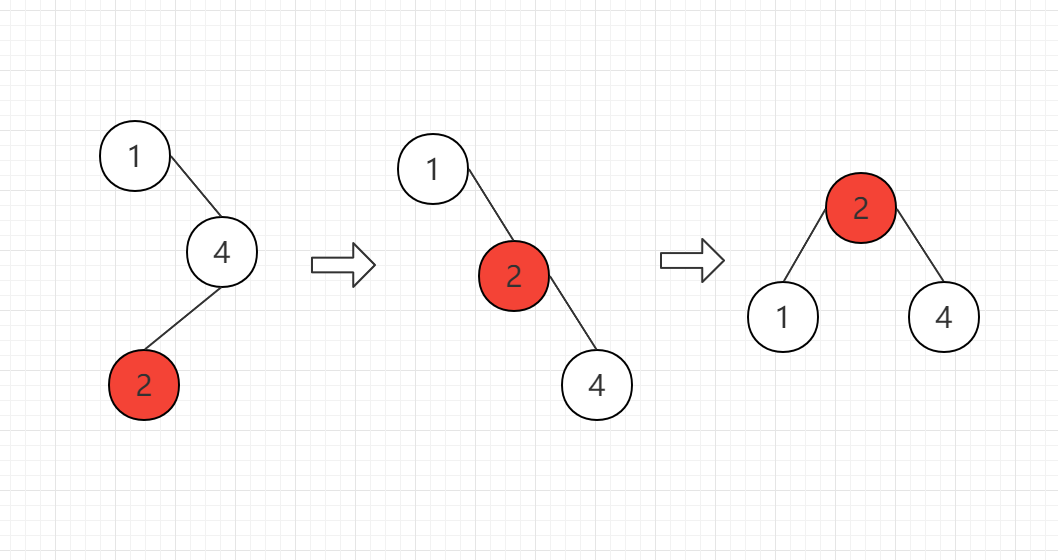
整个复杂点的:

实现代码:
//先右旋再左旋
func (node *TreeNode) rightThenLeftRotate() *TreeNode {
afterRRotateNode := node.Right.rightRotate() //记录右节点右旋后的根节点
node.Right = afterRRotateNode //将本节点的右节点设置为右旋后的根节点(完成右旋操作)
return node.leftRotate() //将节点本身左旋并返回
}调整
通过以上操作介绍,可以知道何时进行何种调整操作,于是乎有了如下方法:
//调整
func (node *TreeNode) adjust() *TreeNode {
//当右子节点深度大于左子节点
// 情况1: 情况2:
// N N
// \ \
// R or R
// \ /
// RR RL
//当左子节点深度大于右子节点
// 情况3: 情况4:
// N N
// / /
// L or L
// / \
// LL LR
if node.Right.getHeight()-node.Left.getHeight() == 2 {
//当右节点的右节点深度大于右节点的左节点时(情况1),否则(情况2)
if node.Right.Right.getHeight() > node.Right.Left.getHeight() {
return node.leftRotate() //左旋(情况1)
} else {
return node.rightThenLeftRotate() //先右旋再左旋(情况2)
}
} else if node.Left.getHeight()-node.Right.getHeight() == 2 {
//当左节点的左子节点深度大于左子节点的右子节点时(情况3),否则(情况4)
if node.Left.Left.getHeight() > node.Left.Right.getHeight() {
return node.rightRotate() //右旋(情况3)
} else {
return node.leftThenRightRotate() //先左旋再右旋(情况4)
}
}
return node
}插入操作
//插入
func (node *TreeNode) insertNode(v int) *TreeNode {
//递归跳出条件:该节点为空,返回需要插入的节点
if node == nil {
return &TreeNode{Value: v, Height: 1}
}
//每次返回都尝试调整
if v < node.Value {
node.Left = node.Left.insertNode(v)
node = node.adjust()
} else if v > node.Value {
node.Right = node.Right.insertNode(v)
node = node.adjust()
} else {
fmt.Println("node exist")
}
//计算高度
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
return node
}至此,插入操作已经完成
删除
删除节点分为两个步骤
- 删除节点
- 重新计算高度并调整节点
其中,删除节点与BST树的删除操作原理大致相同,可以移步之前的文章:
代码:
//删除节点
func (node *TreeNode) deleteNode(v int) *TreeNode {
//递归退出条件:该节点为空
if node == nil {
return node
}
//删除节点
if node.Value > v {
node.Left = node.Left.deleteNode(v)
} else if node.Value < v {
node.Right = node.Right.deleteNode(v)
} else {
if node.Right != nil && node.Left != nil {
maxVal := node.Left.getMax()
node.Value = maxVal
node.Left = node.Left.deleteNode(maxVal)
} else if node.Left != nil {
node = node.Left
} else if node.Right != nil {
node = node.Right
} else {
node = nil
}
}
//调整节点
if node != nil {
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
node = node.adjust()
}
return node
}其他操作
根BST树大同小异,不多赘述
代码:
//获取最大值
func (node *TreeNode) getMax() int {
if node == nil {
return -1
}
if node.Right == nil {
return node.Value
} else {
return node.Right.getMax()
}
}
//获取最小值
func (node *TreeNode) getMin() int {
if node == nil {
return -1
}
if node.Left == nil {
return node.Value
} else {
return node.Left.getMin()
}
}
//查找节点
func findNode(v int, node *TreeNode) *TreeNode {
for {
if node == nil {
return node
}
if node.Value == v {
return node
} else {
if node.Value > v {
node = node.Left
} else {
node = node.Right
}
}
}
}完整实现
avl.go
package avl
import (
"fmt"
)
type TreeNode struct {
Value int
Height int
Left *TreeNode
Right *TreeNode
}
type Tree struct {
Root *TreeNode
}
// Insert 插入
func (t *Tree) Insert(v int) {
t.Root = t.Root.insertNode(v)
}
// Search 查找
func (t *Tree) Search(v int) bool {
node := findNode(v, t.Root)
if node == nil {
return false
} else {
return true
}
}
// Remove 删除
func (t *Tree) Remove(v int) {
t.Root = t.Root.deleteNode(v)
}
// Max 最大值
func (t *Tree) Max() int {
return t.Root.getMax()
}
// Min 最小值
func (t *Tree) Min() int {
return t.Root.getMin()
}
// PreOrderTraverse 前序遍历
func (t *Tree) PreOrderTraverse() {
t.Root.preorder()
}
// InOrderTraverse 中序遍历
func (t *Tree) InOrderTraverse() {
t.Root.inorder()
}
// PostOrderTraverse 后序遍历
func (t *Tree) PostOrderTraverse() {
t.Root.postorder()
}
//获取高度
func (node *TreeNode) getHeight() int {
if node == nil {
return 0
}
return node.Height
}
//左旋
func (node *TreeNode) leftRotate() *TreeNode {
root := node.Right //记录新的根节点
node.Right = root.Left //该节点的右子节点为前右子节点的左子节点
root.Left = node //新根节点的左子节点为该节点
//更新节点高度
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
root.Height = max(root.Left.getHeight(), root.Right.getHeight()) + 1
return root
}
//右旋
func (node *TreeNode) rightRotate() *TreeNode {
root := node.Left //记录新的根节点
node.Left = root.Right //该节点的左子节点为前左子节点的右子节点
root.Right = node //新根节点的右子节点为该节点
//更新节点高度
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
root.Height = max(root.Left.getHeight(), root.Right.getHeight()) + 1
return root
}
//先左旋再右旋
func (node *TreeNode) leftThenRightRotate() *TreeNode {
afterLRotateNode := node.Left.leftRotate() //记录左节点左旋后的根节点
node.Left = afterLRotateNode //将本节点的左节点设置为左旋后的根节点(完成左旋操作)
return node.rightRotate() //将节点本身右旋并返回
}
//先右旋再左旋
func (node *TreeNode) rightThenLeftRotate() *TreeNode {
afterRRotateNode := node.Right.rightRotate() //记录右节点右旋后的根节点
node.Right = afterRRotateNode //将本节点的右节点设置为右旋后的根节点(完成右旋操作)
return node.leftRotate() //将节点本身左旋并返回
}
//插入
func (node *TreeNode) insertNode(v int) *TreeNode {
//递归跳出条件:该节点为空,返回需要插入的节点
if node == nil {
return &TreeNode{Value: v, Height: 1}
}
//每次返回都尝试调整
if v < node.Value {
node.Left = node.Left.insertNode(v)
node = node.adjust()
} else if v > node.Value {
node.Right = node.Right.insertNode(v)
node = node.adjust()
} else {
fmt.Println("node exist")
}
//计算高度
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
return node
}
//调整
func (node *TreeNode) adjust() *TreeNode {
//当右子节点深度大于左子节点
// 情况1: 情况2:
// N N
// \ \
// R or R
// \ /
// RR RL
//当左子节点深度大于右子节点
// 情况3: 情况4:
// N N
// / /
// L or L
// / \
// LL LR
if node.Right.getHeight()-node.Left.getHeight() == 2 {
//当右节点的右节点深度大于右节点的左节点时(情况1),否则(情况2)
if node.Right.Right.getHeight() > node.Right.Left.getHeight() {
return node.leftRotate() //左旋(情况1)
} else {
return node.rightThenLeftRotate() //先右旋再左旋(情况2)
}
} else if node.Left.getHeight()-node.Right.getHeight() == 2 {
//当左节点的左子节点深度大于左子节点的右子节点时(情况3),否则(情况4)
if node.Left.Left.getHeight() > node.Left.Right.getHeight() {
return node.rightRotate() //右旋(情况3)
} else {
return node.leftThenRightRotate() //先左旋再右旋(情况4)
}
}
return node
}
//删除节点
func (node *TreeNode) deleteNode(v int) *TreeNode {
//递归退出条件:该节点为空
if node == nil {
return node
}
//删除节点
if node.Value > v {
node.Left = node.Left.deleteNode(v)
} else if node.Value < v {
node.Right = node.Right.deleteNode(v)
} else {
if node.Right != nil && node.Left != nil {
maxVal := node.Left.getMax()
node.Value = maxVal
node.Left = node.Left.deleteNode(maxVal)
} else if node.Left != nil {
node = node.Left
} else if node.Right != nil {
node = node.Right
} else {
node = nil
}
}
//调整节点
if node != nil {
node.Height = max(node.Left.getHeight(), node.Right.getHeight()) + 1
node = node.adjust()
}
return node
}
//获取最大值
func (node *TreeNode) getMax() int {
if node == nil {
return -1
}
if node.Right == nil {
return node.Value
} else {
return node.Right.getMax()
}
}
//获取最小值
func (node *TreeNode) getMin() int {
if node == nil {
return -1
}
if node.Left == nil {
return node.Value
} else {
return node.Left.getMin()
}
}
//查找节点
func findNode(v int, node *TreeNode) *TreeNode {
for {
if node == nil {
return node
}
if node.Value == v {
return node
} else {
if node.Value > v {
node = node.Left
} else {
node = node.Right
}
}
}
}
//前序遍历
func (node *TreeNode) preorder() {
if node == nil {
return
}
fmt.Print(node.Value)
fmt.Print(" ")
node.Left.preorder()
node.Right.preorder()
}
//中序遍历
func (node *TreeNode) inorder() {
if node == nil {
return
}
node.Left.inorder()
fmt.Print(node.Value)
fmt.Print(" ")
node.Right.inorder()
}
//后序遍历
func (node *TreeNode) postorder() {
if node == nil {
return
}
node.Left.postorder()
node.Right.postorder()
fmt.Print(node.Value)
fmt.Print(" ")
}
//两数最大值
func max(a int, b int) int {
if a > b {
return a
} else {
return b
}
}
avl_test.go(测试)
package avl
import (
"fmt"
"testing"
)
func Test_AVLTree(t *testing.T){
avl := new(Tree)
avl.Insert(8)
avl.Insert(3)
avl.Insert(10)
avl.Insert(1)
avl.Insert(6)
avl.Insert(14)
avl.Insert(4)
avl.Insert(7)
avl.Insert(13)
fmt.Println("search 7:", avl.Search(7))
fmt.Println("search 11", avl.Search(11))
fmt.Println("PreOrder Traverse:")
avl.PreOrderTraverse()
fmt.Println()
fmt.Println("InOrder Traverse:")
avl.InOrderTraverse()
fmt.Println()
fmt.Println("PostOrder Traverse:")
avl.PostOrderTraverse()
fmt.Println()
fmt.Println("before remove:")
avl.InOrderTraverse()
fmt.Println()
avl.Remove(3)
fmt.Println("after remove 3:")
avl.InOrderTraverse()
fmt.Println()
}
