介绍
二叉查找树(英语:Binary Search Tree),也称为二叉查找树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构,用于构建更为抽象的数据结构,如集合、多重集、关联数组等。
二叉查找树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列,一个无序序列可以透过建构一棵二叉查找树变成一个有序序列,建构树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索、插入、删除的复杂度等于树高,期望O(log n),最坏O(n)(数列有序,树退化成线性表)。
(以上内容摘自wikipedia)
简而言之,就是左边的节点一定比根节点小,右边的节点一定比根节点大,如下图:
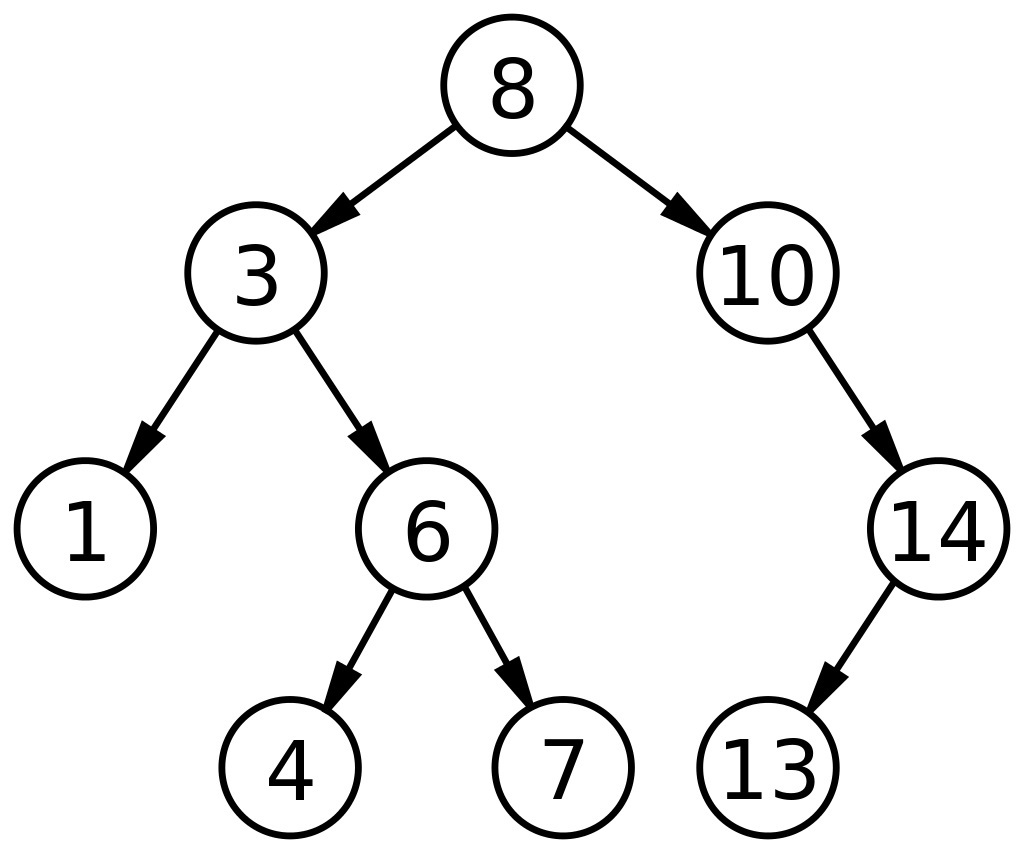
相关操作
插入
插入过程比较简单,一路递归下去,当新节点小于该节点,往左边插入,否则往右边插入
func insertNode(node *TreeNode, newNode *TreeNode) {
//当新节点小于该节点,左边插入,否则右边插入
if newNode.Value < node.Value {
if node.Left != nil {
insertNode(node.Left, newNode)
} else {
node.Left = newNode
}
} else {
if node.Right != nil {
insertNode(node.Right, newNode)
} else {
node.Right = newNode
}
}
}查找
查找过程也比较简单,与节点进行比对,小的往左走大的往右走知道找到该节点或找不到该节点
func findNode(v int, node *TreeNode) *TreeNode {
for {
if node == nil {
return node
}
if node.Value == v {
return node
} else {
if node.Value > v {
node = node.Left
} else {
node = node.Right
}
}
}
}最值
这个就更简单了,最小值往左边遍历,最大值往右边遍历,到头就是了
// Max 最大值
func (b *BinarySearchTree) Max() int {
node := b.Root
for {
if node.Right != nil {
node = node.Right
} else {
return node.Value
}
}
}
// Min 最小值
func (b *BinarySearchTree) Min() int {
node := b.Root
for {
if node.Left != nil {
node = node.Left
} else {
return node.Value
}
}
}删除
BST里面最复杂的应该就是删除操作了,通过观察BST,我们能够发现,需要删除的节点存在四种情况:
- 没有子节点
- 只有左节点
- 只有右节点
- 左右节点都有
对此,我们需要分别处理
对于情况1,只需要删除该节点即可:
对于情况2,删除该节点,并将该节点提升至左节点
对于情况3,删除该节点,并将该节点提升至右节点
情况4需要做特殊说明:

如上所示,假如我们需要删除3号节点,满足情况4,需要先将该节点删除
删除后可存在两种操作,均可以使该树满足BST条件:
- 找到左子树的最大节点,并将该节点提升到节点3的位置
- 找到右子树的最小节点,并将该节点提升到节点3的位置
以上操作后,根据BST的性质,必然不会破坏该树的结构,不信的可以自行证明
//删除节点
func deleteNode(node *TreeNode, v int) *TreeNode {
if node == nil {
return node
}
if node.Value > v {
node.Left = deleteNode(node.Left, v)
return node
}
if node.Value < v {
node.Right = deleteNode(node.Right, v)
return node
}
//情况1:没有子节点
if node.Left == nil && node.Right == nil {
node = nil
return node
}
//情况2:右子节点为空,即只有左子节点,提升左子节点
if node.Right == nil {
node = node.Left
return node
}
//情况3:左子节点为空,即只有右子节点,提升右子节点
if node.Left == nil {
node = node.Right
return node
}
//情况4:左右节点都部位空,将该节点与左子树最大或者右子树最小节点进行替换,替换后删除节点
if node.Right != nil && node.Left != nil {
maxVal := findMaxInLeft(node.Left)
node.Value = maxVal
node.Left = deleteNode(node.Left, maxVal)
return node
}
return node
}
//查找左节点最大值
func findMaxInLeft(leftNode *TreeNode) int {
for {
if leftNode.Right != nil {
leftNode = leftNode.Right
} else {
return leftNode.Value
}
}
}Golang实现
bst.go
package bst
import "fmt"
type TreeNode struct {
Value int
Left *TreeNode
Right *TreeNode
}
type BinarySearchTree struct {
Root *TreeNode
}
// Insert 插入
func (b *BinarySearchTree) Insert(v int) {
if b.Root == nil {
b.Root = &TreeNode{Value: v}
return
}
insertNode(b.Root, &TreeNode{Value: v})
}
// Remove 删除
func (b *BinarySearchTree) Remove(v int) {
deleteNode(b.Root, v)
}
// Search 查找
func (b *BinarySearchTree) Search(v int) bool {
node := findNode(v, b.Root)
if node == nil {
return false
} else {
return true
}
}
// Max 最大值
func (b *BinarySearchTree) Max() int {
node := b.Root
for {
if node.Right != nil {
node = node.Right
} else {
return node.Value
}
}
}
// Min 最小值
func (b *BinarySearchTree) Min() int {
node := b.Root
for {
if node.Left != nil {
node = node.Left
} else {
return node.Value
}
}
}
// PreOrderTraverse 前序遍历
func (b *BinarySearchTree) PreOrderTraverse() {
preorder(b.Root)
fmt.Println()
}
// InOrderTraverse 中序遍历
func (b *BinarySearchTree) InOrderTraverse() {
inorder(b.Root)
fmt.Println()
}
// PostOrderTraverse 后序遍历
func (b *BinarySearchTree) PostOrderTraverse() {
postorder(b.Root)
fmt.Println()
}
//插入节点
func insertNode(node *TreeNode, newNode *TreeNode) {
//当新节点小于该节点,左边插入,否则右边插入
if newNode.Value < node.Value {
if node.Left != nil {
insertNode(node.Left, newNode)
} else {
node.Left = newNode
}
} else {
if node.Right != nil {
insertNode(node.Right, newNode)
} else {
node.Right = newNode
}
}
}
//删除节点
func deleteNode(node *TreeNode, v int) *TreeNode {
if node == nil {
return node
}
if node.Value > v {
node.Left = deleteNode(node.Left, v)
return node
}
if node.Value < v {
node.Right = deleteNode(node.Right, v)
return node
}
//情况1:没有子节点
if node.Left == nil && node.Right == nil {
node = nil
return node
}
//情况2:右子节点为空,即只有左子节点,提升左子节点
if node.Right == nil {
node = node.Left
return node
}
//情况3:左子节点为空,即只有右子节点,提升右子节点
if node.Left == nil {
node = node.Right
return node
}
//情况4:左右节点都部位空,将该节点与左子树最大或者右子树最小节点进行替换,替换后删除节点
if node.Right != nil && node.Left != nil {
maxVal := findMaxInLeft(node.Left)
node.Value = maxVal
node.Left = deleteNode(node.Left, maxVal)
return node
}
return node
}
//查找左节点最大值
func findMaxInLeft(leftNode *TreeNode) int {
for {
if leftNode.Right != nil {
leftNode = leftNode.Right
} else {
return leftNode.Value
}
}
}
//查找节点
func findNode(v int, node *TreeNode) *TreeNode {
for {
if node == nil {
return node
}
if node.Value == v {
return node
} else {
if node.Value > v {
node = node.Left
} else {
node = node.Right
}
}
}
}
//前序遍历
func preorder(node *TreeNode) {
if node == nil {
return
}
fmt.Print(node.Value)
fmt.Print(" ")
preorder(node.Left)
preorder(node.Right)
}
//中序遍历
func inorder(node *TreeNode) {
if node == nil {
return
}
inorder(node.Left)
fmt.Print(node.Value)
fmt.Print(" ")
inorder(node.Right)
}
//后序遍历
func postorder(node *TreeNode) {
if node == nil {
return
}
postorder(node.Left)
postorder(node.Right)
fmt.Print(node.Value)
fmt.Print(" ")
}
bst_test.go (测试代码)
package bst
import (
"fmt"
"testing"
)
func Test_BinarySearchTree(t *testing.T) {
bst := new(BinarySearchTree)
bst.Insert(8)
bst.Insert(3)
bst.Insert(10)
bst.Insert(1)
bst.Insert(6)
bst.Insert(14)
bst.Insert(4)
bst.Insert(7)
bst.Insert(13)
fmt.Println("search 7:", bst.Search(7))
fmt.Println("search 11", bst.Search(11))
fmt.Println("PreOrder Traverse:")
bst.PreOrderTraverse()
fmt.Println("InOrder Traverse:")
bst.InOrderTraverse()
fmt.Println("PostOrder Traverse:")
bst.PostOrderTraverse()
fmt.Println("before remove:")
bst.InOrderTraverse()
bst.Remove(3)
fmt.Println("before remove 3:")
bst.InOrderTraverse()
}
Leetcode 450. 删除二叉搜索树中的节点
题目描述
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
题解
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
func deleteNode(root *TreeNode, key int) *TreeNode {
if root == nil {
return root
}
if root.Val > key {
root.Left = deleteNode(root.Left, key)
return root
}
if root.Val < key {
root.Right = deleteNode(root.Right, key)
return root
}
if root.Left == nil && root.Right == nil {
root = nil
return root
}
if root.Left == nil {
root = root.Right
return root
}
if root.Right == nil {
root = root.Left
return root
}
if root.Right != nil && root.Left != nil {
maxVal := findMaxInLeft(root.Left)
root.Val = maxVal
root.Left = deleteNode(root.Left, maxVal)
return root
}
return root
}
func findMaxInLeft(leftNode *TreeNode) int {
for {
if leftNode.Right != nil {
leftNode = leftNode.Right
} else {
return leftNode.Val
}
}
}结果
执行用时:12 ms, 在所有 Go 提交中击败了85.25%的用户
内存消耗:6.9 MB, 在所有 Go 提交中击败了100.00%的用户
