介绍

归并排序是创建在归并操作上的一种有效的排序算法，效率为O(nlogn)，1945年由冯·诺伊曼首次提出。归并排序算法主要依赖归并(Merge)操作。归并操作指的是将两个已经排序的序列合并成一个序列的操作。本文主要介绍递归法。

时间复杂度：

• 最好情况：O(nlogn)
• 平均情况：O(nlogn)
• 最坏情况：O(nlogn)

稳定性：稳定

额外的空间：O(n)

过程

递归操作

1. 将待排序元素分为大致相同的两个子集合
2. 重复步骤1直到每个子集合仅包含1个或0个元素
3. 对两个子集合分别进行排序
4. 合并两个已排序的子序列
5. 得到排序结果

归并操作

1. 创建左右两个临时数组
2. 依次比较两个数组的元素，并将较小的元素放回原数组
3. 重复步骤2直到所有元素都放回原数组
4. 合并完成

以上内容可能比较抽象（主要是我表达能力比较垃圾），用图示可能比较好理解：

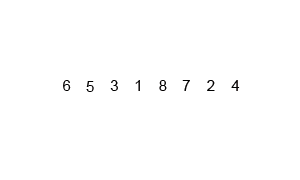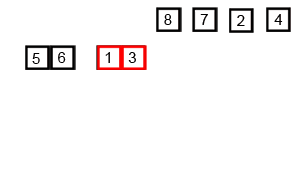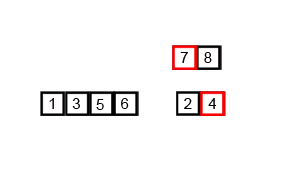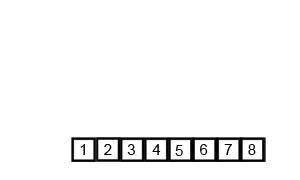
宏观过程：

Java实现

/*
 * MergeSort.java:归并排序（递归实现）
 */
import java.util.Arrays;

public class MergeSort {
    public static void main(String[] args) {
        int[] a = new int[]{9, 2, 5, 6, 7, 2, 4, 5};
        sort(a, 0, a.length - 1);
        System.out.println(Arrays.toString(a));
    }

    private static void sort(int[] arr, int left, int right) {
        //递归跳出条件：左边索引大于右边索引
        if (left >= right) {
            return;
        }
        int mid = (right + left) / 2;//中间位置索引
        //从左往右递归
        sort(arr, left, mid);
        sort(arr, mid + 1, right);
        merge(arr, left, right, mid);//合并已排序好的数组

    }

    /**
     * 归并操作
     * @param arr 待排序数组
     * @param left 数组左边索引
     * @param right 数组右边索引
     * @param mid 数组中间索引
     */
    private static void merge(int[] arr, int left, int right, int mid) {
        int leftLength = mid - left + 1;//左边数组长度
        int rightLength = right - mid;//右边数组长度
        //注意：int最大值标记位用于合并操作时，当遍历到某一数组（左或右）最后一位时，无法继续与另一位比较，因此引入此标记位用于比较
        int[] leftArr = new int[leftLength + 1];//左边临时数组，增加一位为int最大值标记位
        int[] rightArr = new int[rightLength + 1];//右边临时数组，增加一位为int最大值标记位
        for (int i = 0; i < leftLength; i++) {
            leftArr[i] = arr[left + i];//将元素存入临时数组
        }
        for (int i = 0; i < rightLength; i++) {
            rightArr[i] = arr[mid + i + 1];//将元素存入临时数组
        }
        leftArr[leftLength] = Integer.MAX_VALUE;//临时数组最后一位取int最大值
        rightArr[rightLength] = Integer.MAX_VALUE;//临时数组最后一位取int最大值
        int i = 0, j = 0;//左右临时数组索引标记
        //合并数组，依次将小的放在数组左边
        for (int k = left; k <= right; k++) {
            if (leftArr[i] <= rightArr[j]) {
                arr[k] = leftArr[i];
                i++;
            } else {
                arr[k] = rightArr[j];
                j++;
            }
        }
    }
}